Bloque 1 · Ingeniería Térmica I · Transferencia de Calor.
En estas Prácticas se aprende a medir los coeficientes de transferencia de calor por conducción de los materiales que habitualmente se emplean tanto en Ingeniería como en Arquitectura, ya sea como aislamientos o como buenos transmisores del calor.
También se aprende a medir el coeficiente de transferencia de calor por convección entre dichos materiales y aire, en pared plana y se establece un procedimiento para medir la resistencia térmica de paredes de varias capas y para hacer una estimación de la resistencia térmica de contacto.
Además, en esta Práctica los estudiantes se familiarizan con los órdenes de magnitud de los coeficientes de transferencia de calor por conducción y por convección de los materiales, así como con el uso de los procedimientos más básicos empleados en el Laboratorio de Ingeniería Térmica o Termotecnia, entre los que se encuentran el uso de termopares, termostatos, fuentes de alimentación eléctrica y transferencia de datos hacia el ordenador y su tratamiento, una vez en éste.
El material para la realización de la Práctica consiste en una cámara calorimétrica en cuyo interior se coloca una resistencia eléctrica (una bombilla) y un termopar, que envía la información de la temperatura en el interior de la cámara calorimétrica a un termostato. La cámara calorimétrica se cierra por su parte superior con la probeta del material cuyas propiedades térmicas (k y h) se quieren medir. Hay que evitar que la radiación de la bombilla incida directamente en la probeta. Para ello, se coloca un apantallamiento de aluminio en el interior de la cámara calorimétrica, sobre la bombilla.
A la bombilla llega la energía eléctrica desde una fuente de alimentación en la que se pueden medir, en todo momento, la tensión (en V) y la intensidad de la corriente (en A) que circula por el circuito. En serie con la bombilla se coloca el termostato que recibe la señal del termopar colocado en el interior de la cámara calorimétrica y en él se selecciona la temperatura objetivo (unos 40 °C), de modo que cuando la temperatura en el interior de la cámara calorimétrica sea menor, el termostato cierra el circuito (circulando entonces corriente por él) y cuando sea mayor, lo abre.
Determinación del calor que atraviesa la probeta.
Con un cronómetro se mide el tiempo durante el que la bombilla permanece encendida (t_I) y también el tiempo durante el que permanece apagada (t_O). La energía intercambiada como trabajo de rozamiento y posteriormente como calor por la bombilla durante el tiempo que está encendida, Q_I, viene dada por
Q_I = V I t_I
Este es el calor que atraviesa la probeta, ya que la cámara calorimétrica es prácticamente adiabática. Pero este calor que atraviesa la probeta no está gobernado por ningún termostato, y está atravesándola tanto durante el tiempo que la bombilla permanece encendida, t_I, como durante el tiempo en que la bombilla permanece apagada, t_O, por lo que el calor que por unidad de tiempo atraviesa la probeta, \dot{Q}, viene dado por
\dot{Q}=\frac{V I t_I}{t_I+t_O}
Determinación del coeficiente de transferencia de calor por conducción o coeficiente de conducción.
De la Ecuación de Fourier se tiene
\dot{Q}=-kA\frac{\Delta T}{e}
Sustituyendo, resulta,
\frac{V I t_I}{t_I+t_O}=-kA\frac{\Delta T}{e}
Y despejando k,
k=\frac{e V I t_I}{A \left(T_1-T_2\right) \left(t_I+t_O\right)}
Es necesario, pues, medir la temperatura en la superficie externa de la probeta, T_2. Para ello se emplea un termopar.
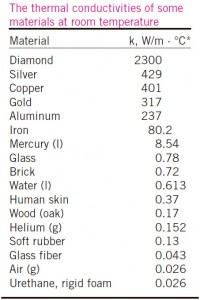
En la siguiente Tabla se ofrecen los valores del coeficiente de transferencia de calor por conducción para algunas sustancias comunes (de Çengel, Y. Heat and Mass Transfer):
Determinación del coeficiente de transferencia de calor por convección o coeficiente de convección.
Para obtener el coeficiente de convección, h, basta con considerar el calor intercambiado entre la superficie y el aire, que viene dado por la Ecuación del Enfriamiento de Newton como
\dot{Q}=h A \left(T_s-T_{\infty }\right)
Sustituyendo el valor obtenido para \dot{Q}
\frac{V I t_I}{t_I+t_O}=h A \left(T_s-T_{\infty }\right)
Y despejando h,
h=\frac{V I t_I}{A \left(t_I+t_O\right) \left(T_s-T_{\infty }\right)}

Hay más información en la Web de Leybold.