Bloque 2 · Ingeniería Térmica I · Propiedades Termodinámicas de las sustancias puras.
En estas prácticas se aprende a dibujar las líneas isotermas de una sustancia real pura, apreciando el inicio de la campana de saturación por la aparición de la fase líquida e identificando el estado de vapor saturado para cada presión y temperatura. También se puede apreciar la dependencia entre presión y temperatura en los cambios de fase. Se puede, también, encontrar el punto crítico apreciando el fenómeno de opalescencia que tiene lugar en su entorno y la inexistente transición de fase en la zona supercrítica apreciando, también, la bajísima compresibilidad de la fase supercrítica.
Para terminar, se puede también calcular la masa de SF_6 en el interior del tubo empleando el Factor de Compresibilidad, Z, obtenido de la Gráfica de Compresibilidad.
La sustancia con la que se trabaja, por la accesibilidad de su punto crítico, es Hexafluoruro de Azufre, SF_6, cuyas propiedades en el punto crítico son:
- M=146,05 \text{ } kg/kmol.
- p_C =37,59 \text{ } bar.
- t_C=45,5 \textit{$\, ^oC$}.
Es recomendable asisitir a la realización de la práctica con un ordenador con Microsoft Excell instalado (en lugar de papel milimetrado), o similar, que permita la realización de gráficos a partir de los datos obtenidos experimentalmente, así como de las Gráficas de Compresibilidad de la Bibliografía.
Obtención de líneas isotermas del SF_6.
Lo primero que hay que hacer es bajar el nivel del mercurio en el tubo que contiene el SF_6 hasta el nivel más bajo. Se observa en el manómetro que la presión del SF_6 disminuye. El manómetro mide, obviamente, la presión manométrica, p_m. La presión absoluta, p, que habrá que considerar es
p=p_a+p_m
por lo que será necesario considerar la presión atmosférica p_a que habrá que leer en el barómetro de mercurio. La densidad del mercurio es \rho_\text{Hg} =13595 \text{ } kg/m^3. Así, resultará para la presión atmosférica,
p_a=\rho_\text{Hg}gz_\text{Hg}
donde z_\text{Hg} es la altura, en m, de la columna de mercurio en el barómetro. Para leer en el barómetro hay que asegurarse de que el tapón exterior no obstruye el paso del aire y también de que el tapón interior no obstruye el paso del mercurio. Con todo lo anterior, la presión absoluta del SF_6 será
p=\rho_\text{Hg}gz_\text{Hg}+p_m
A continuación se establece una temperatura objetivo en el termostato del baño de agua. El agua circula por el exterior del tubo en el que está contenido el SF_6 y en unos minutos se puede comprobar, en el termómetro de alcohol cuyo bulbo está situado en el interior del tubo externo, que el agua alcanza la temperatura objetivo. En ese momento se comienza a girar el volante, haciendo que el mercurio se eleve y aumentando la presión en el manómetro. Para poder dibujar la línea isoterma en el diagrama p-V hay que elevar la presión lentamente ya que se si hace deprisa la compresión del SF_6 es adiabática, con el consiguiente aumento de temperatura. En ese caso hay que esperar unos segundos a que el SF_6 se enfríe. Así, se va comprimiendo el SF_6 deteniéndose a intervalos de volumen y anotando los valores de p_m y V que permitan, posteriormente, dibujar una gráfica como una sucesión de puntos.
Al ir comprimiendo llega un momento en el que se aprecia la formación de líquido sobre el mercurio. Es, entonces, cuando se alcanza la curva de saturación del vapor. A partir de entonces, aunque se disminuya el volumen la presión no cambiará, ya que la temperatura tampoco cambia. A medida que se disminuye el volumen se observa que la masa de líquido es cada vez mayor. No es necesario condensar todo el SF_6. Es más, no se debe condensar todo el SF_6 ya que si se condensa todo, una pequeña disminución en el volumen daría lugar a una presión tan grande que el tubo de vidrio que lo contiene, aunque es muy grueso, podría romperse.
En Excell (o similar) se va tomando nota de las presiones y volúmenes en cada estado. La tabla que se construye, para cada temperatura, tiene un aspecto similar a la que se indica a continuación:
| Medida | V \text{ } (ml) | p \text{ } (bar)@t_1 | p \text{ } (bar)@t_2 | p \text{ } (bar)@t_3 | p \text{ } (bar)@t_4 |
| 1 | |||||
| 2 | |||||
| i | |||||
| n |
A continuación se cambia la temperatura objetivo del baño de agua en el termostato y se espera unos minutos hasta que el termómetro de alcohol en el tubo externo la indique. Una vez se alcanza la temperatura objetivo en el baño de agua, se completa la construcción de la siguiente columna de la tabla en Excell, tomando la precaución de hacer las medidas en los mismos volúmenes, salvo para el volumen en que sobrevenga la saturación, que se anota explícitamente y que no tiene por qué haberse anotado en temperaturas anteriores (por desconocerse), debiendo dar lugar a una nueva fila en la tabla. La saturación sobreviene a volúmenes menores a medida que se aumenta la temperatura, por lo que en cada temperatura habrá una casilla que no tenga correspondencia con las de temperaturas anteriores, que será la del volumen correspondiente a la saturación.
Una vez completada la tabla se puede indicar a Excell que dibuje la gráfica que representa p en ordenadas y V en abscisas para cada temperatura. La gráfica obtenida tiene que ser similar a la que se presenta a continuación, en la que se dibujan varias isotermas, incluida la de temperatura t_C y una de temperatura superior a la crítica.
Determinación de la masa de SF_6 en el tubo.
Para calcular la masa de SF_6 en el interior del tubo es necesario recurrir al factor de compresibilidad, Z. Efectivamente, como se ha visto
p V=Z m R T
De aquí
m=\frac{p V}{Z R T}
En esta ecuación hay que tener en cuenta que R=\frac{\bar{R}}{M}, siendo \bar{R}=8,314\text{ } kJ/kmol\text{ }K.
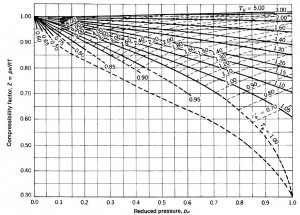
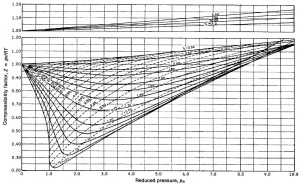
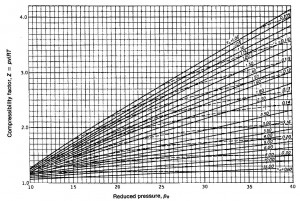
Basta, pues, con elegir un estado de entre los medidos anteriormente a partir de su presión reducida, p_R=p/p_C, y de su temperatura reducida, T_R=T/T_C, obtener, de la gráfica de compresibilidad, el valor de Z que corresponda, y sustituir en la expresión de m.
Se incluye, a continuación, la gráfica de compresibilidad de Fundamentos de Termodinámica Técnica, de Moran, M. y Shapiro, H.
Determinación de las isotermas reducidas y de las líneas de volumen pseudorreducido constante en la gráfica de compresibilidad generalizada.
Para calcular los puntos de cada isoterma reducida en la carta de compresibilidad generalizada hay que determinar, para cada presión, p, su correspondiente presión reducida, p_R. Y para cada volumen, el correspondiente si el comportamiento fuese como gas ideal para, a partir de ahí, determinar la correspondiente Z, que viene dada por
Z=\frac{V}{V_{\text{id}}}=\frac{V}{\frac{m R T}{p}}=\frac{p V}{m R T}
Así, los puntos de las isotermas reducidas se pueden obtener de la tabla anterior, añadiendo las columnas que se indican a continuación:
| Medida | p_R @t_1 | Z@t_1 | p_R @t_2 | Z@t_2 | p_R @t_3 | Z@t_3 | p_R @t_4 | Z@t_4 |
| 1 | ||||||||
| 2 | ||||||||
| i | ||||||||
| n |
Del mismo modo, para las líneas de volumen pseudorreducido constante, v'_R, como
v'_R=\frac{V}{V_{c,\text{id}}}=\frac{V}{\frac{m R T_C}{p_C}}=\frac{p_C V}{m R T_C}
se pueden añadir a la tabla de datos las siguientes columnas
| Medida | v'_R @t_1 | Z@t_1 | v'_R @t_2 | Z@t_2 | v'_R @t_3 | Z@t_3 | v'_R @t_4 | Z@t_4 |
| 1 | ||||||||
| 2 | ||||||||
| i | ||||||||
| n |
Ya a partir de aquí, tan sólo hay que hacer que Excell dibuje la gráfica de Z = Z(p_R) para cada T_R y para cada v'_R.