Previamente al Balance de Energía es necesario hacer un análisis dinámico.
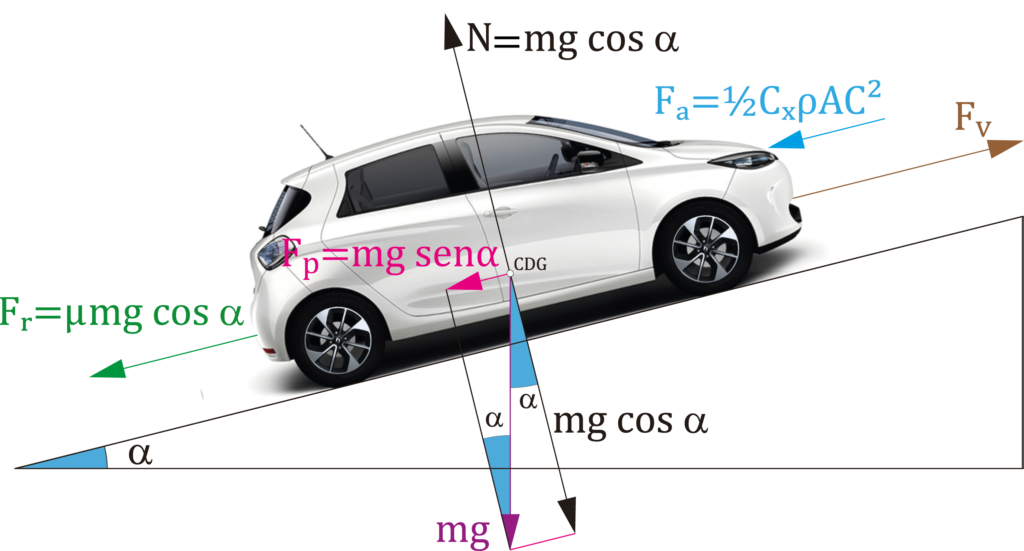
En la figura se muestran todas las fuerzas que actúan en un vehículo en movimiento.
FUERZA NECESARIA PARA VENCER LA RESISTENCIA A LA RODADURA.
La fuerza necesaria para vencer la resistencia de rodadura, F_r, es
F_r=\mu\times N
donde \mu es el coeficiente de resistencia a la rodadura, y N es la componente normal al suelo, mg cos \alpha, del peso del vehículo. Así,
F_r=\mu mg cos \alpha
FUERZA EN LA SUBIDA (O BAJADA) DE UNA PENDIENTE
La fuerza en la subida (o bajada) de una pendiente, F_p, es
F_p= \pm mg sen\alpha
En esta ecuación se emplea el signo “-” cuando F_p y F_v tengan distinto sentido (cuando el vehículo sube), y “+” cuando tengan el mismo sentido (cuando el vehículo baja).
FUERZA NECESARIA PARA VENCER LA RESISTENCIA AERODINÁMICA
La fuerza necesaria para vencer la resistencia aerodinámica, F_a, es
F_a= \frac{1}{2}C_x\rho AC^2
donde C_x es el coeficiente de resistencia aerodinámica, \rho es la densidad del aire, A es la superficie frontal del vehículo y C es la velocidad a la que se mueve el vehículo en relación con la velocidad del aire en cuyo seno se mueve.
El aire atmosférico cumple bastante bien la ecuación de estado de gas ideal, por lo que se puede escribir
pv=RT
Y como v=1/\rho, queda \frac{p}{\rho}=RT, de donde resulta
\rho = \frac{p}{RT},
quedando, para la fuerza necesaria para vencer la resistencia aerodinámica,
F_a= \frac{1}{2} C_x \frac{p}{RT} A C^2
FUERZA EJERCIDA POR EL VEHÍCULO
En la figura, es F_v.
ECUACIÓN DE NEWTON
\Sigma \overrightarrow{F}= m \frac{d \overrightarrow{C}}{dt}
Aunque es mandatorio el empleo de vectores, como todas las fuerzas se encuentran en la misma dirección, se puede trabajar escalarmente considerando simplemente sus signos, resultando,
F_v - \left(\pm mg sen\alpha + \mu mg cos \alpha + \frac{1}{2} C_x \frac{p}{RT} A C^2 \right) = m \frac{dC}{dt}
Multiplicando la ecuación anterior por la velocidad, C ,
F_v C - \left(\pm mgC sen\alpha + \mu mgC cos \alpha + \frac{1}{2} C_x \frac{p}{RT} A C^3 \right) = m C \frac{dC}{dt}
En esta ecuación, F_v C es la potencia desarrollada por el vehículo, \pm mgC sen\alpha es la potencia requerida para subir la pendiente (o aportada en la bajada, lo que es importante en los vehículos eléctricos, que pueden emplear la energía generada para cargar baterías), \mu mgC cos \alpha es la potencia requerida para vencer la resistencia a la rodadura, \frac{1}{2} C_x \frac{p}{RT} A C^3 es la potencia requerida para vencer la resistencia aerodinámica (nótese que aumenta con el cubo de la velocidad) y m C \frac{dC}{dt} es la potencia requerida en la aceleración u obtenida en la frenada que, en el caso de los vehículos eléctricos, se puede emplear en la carga de las baterías.