Archivo del autor: Juan-Ramón Muñoz Rico
¿Por qué la evolución de infectados por el COVID-19 es exponencial?
Desde el 14 de Marzo nos encontramos en España en Estado de Alarma por la preocupante evolución del número de contagiados por el COVID-19, que ha mostrado ser exponencial.
¿Por qué la evolución del número de contagios del del COVID-19 es exponencial? En esta página Web se muestran algunas animaciones de todos los escenarios posibles. Las animaciones siempre se agradecen pero en Ingeniería necesitamos ponerles números a las cosas.
Vamos a ello:
Aparecen más infectados cuantos más infectados haya.
Llamando [i] al número total de infectados (lo que en Química sería la “concentración” de infectados), esto lleva a admitir que la velocidad de contagio, \frac{d[i]}{dt}, es proporcional al número de contagiados, k[i]. La Cinética Química del número de contagiados corresponde, si esto es así, a la de una reacción de orden 1, es decir
\frac{d[i]}{dt}=k[i]
Se trata de una ecuación diferencial de variables separables en la que la constante k tiene unidades de \frac{1}{t} . No es necesario, en este caso, recurrir al Sistema Internacional y expresar el tiempo en segundos. Basta con expresarlo en días, ya que el balance de infectados se ofrece diariamente. Por tanto, las unidades de k serán \frac{1}{\text{dias}} . La ecuación diferencial anterior lleva a
\frac{d[i]}{[i]} = k dt
Integrando entre dos concentraciones de infectados, [i]_1 e [i]_2 , reportadas en dos instantes, t_1 e t_2 , resulta
\int _{[i]_1}^{[i]_2}\frac{d[i]}{[i]} = \int _{t_1}^{t_2} k dt
Considerando k como constante, resulta
\ln \frac{[i]_2}{[i]_1}=k \left(t_2-t_1\right)
Y operando, resulta
\frac{[i]_2}{[i]_1}=e^{k \left(t_2-t_1\right)}
Nuestro problema, ahora, es determinar el valor de la constante k . Para ello, hemos de recurrir a los datos medidos de dos instantes cualesquiera. En Web del Ministerio de Sanidad se pueden encontrar datos fiables. Basta con elegir los datos correspondientes a dos días, cualesquiera, y sustituir en la ecuación
k=\frac{\ln \frac{[i]_2}{[i]_1}}{t_2-t_1}
Tomando los datos del día 16 de Marzo, cuando [i]_1=9191 infectados, y del 25 de Marzo (a 9 días de distancia), cuando [i]_2=47610 infectados, resulta
k=\frac{ln \frac{47610 \text{infectados}}{9191 \text{infectados}}}{9 \text{días}}=0, 1828 \text{días}^{-1}
Así pues, la ecuación que da una idea de la evolución de la infección es
[i]_2=[i]_1e^{0,1828 \left(t_2-t_1\right)}
donde hay que escribir los tiempos en días.
A continuación se muestra la representación gráfica de esta ecuación. Como se puede ver, es una representación típica de una ecuación exponencial. Pasada una primera fase inicial, en la que el número de infectados aumenta lentamente, pasa a una fase de aumento muy rápido… y rapidísimo a medida que avanza el tiempo.
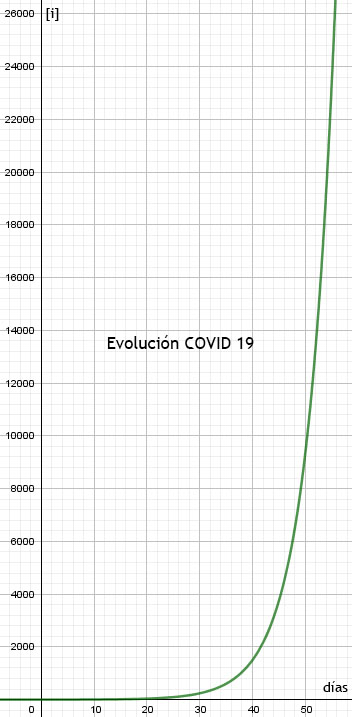
Como se puede deducir de la forma de la curva, el aumento del número de infectados, [i], es muy lento en los primeros días. Esto es lo que ha enmascarado la epidemia y lo que ha confundido a los expertos: al tratarse de un virus nuevo, nadie era capaz de imaginarse su altísima contagiosidad. En España no miramos a la evolución del COVID-19 en otros países (o sí) y jamás pensamos que íbamos a seguir el mismo camino. La cuestión es que aquí estamos.
Las actuaciones, a la vista de la forma de la curva, se encaminan a sacarla de la zona exponencial. Las primeras medidas, en las que estamos, tratan de encontrar un cambio en la ya leve curvatura de la gráfica, es decir, una inflexión. Una inflexión que será muy tenue, pero aparecerá. Y, a partir de ahí, a encontrar el máximo de la función. A partir del máximo, nos encontraremos en ya en la zona de decrecimiento de los contagios. A partir de ahí, iremos “viendo la luz”.
En este sentido, la declaración del Estado de Alarma y las medidas de contención son mucho más que acertadas y pertinentes. Hay que “doblar” (textual del Prof. Dr. Fernando Simón Soria) la ecuación exponencial; véanse los escenarios recreados en las animaciones de Washington Post que indiqué en el comienzo de esta misma entrada.
¿Cuál es el coste energético eléctrico del Estado de Alarma decretado en España debido a la epidemia de COVID 19?
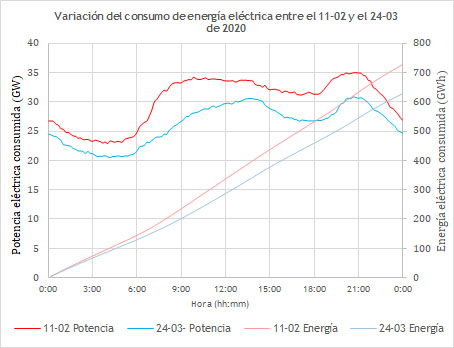
El 11 de Febrero se consumió una energía de 726,369 GWh.
El 24 de Marzo se consumió una energía de 628,748 GWh.
El parón energético entre esos días es 97,621 GWh.
El coste económico asociado, considerando un precio medio de 0,15 €/kWh asciende a 14643175 € (entre esos días).
¿Qué avión estoy viendo en el cielo? ¿Dónde están los aviones? ¿A qué velocidad van? ¿A qué altura? ¿De qué compañía son? ¿Dónde van? ¿De dónde vienen? ¿A qué hora han salido? ¿A qué hora llegarán?
Pues aquí los ves.
Si estás en el ordenador, en casa, y no tienes una ventana cerca, instálate esta App en el teléfono, sal y mira al cielo. Si quieres saber mejor lo que te dice la App, ten en cuenta que 1 ft = 0,3048 m y que 1 kt = 1,852 km/h
Balance energético en un automóvil.
Previamente al Balance de Energía es necesario hacer un análisis dinámico.
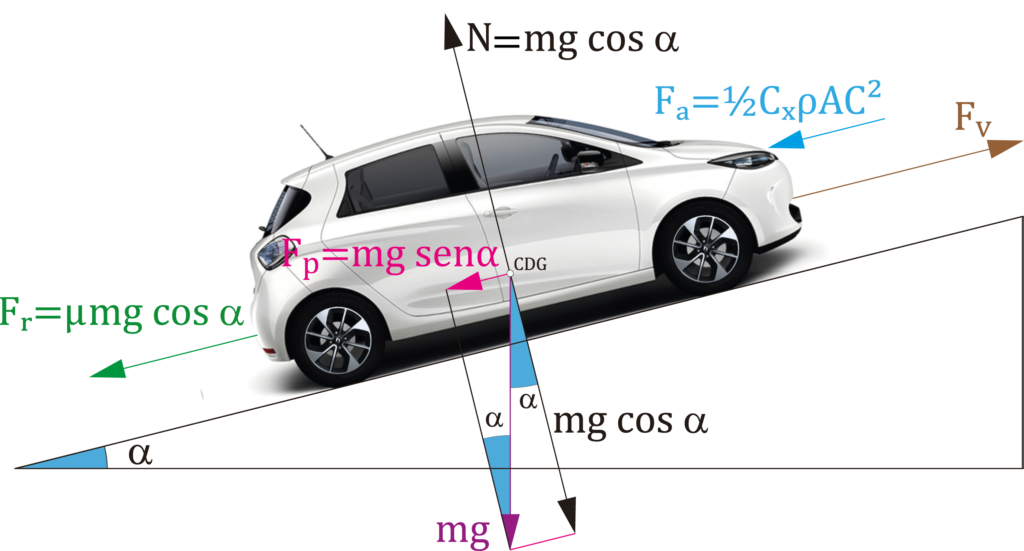
En la figura se muestran todas las fuerzas que actúan en un vehículo en movimiento.
FUERZA NECESARIA PARA VENCER LA RESISTENCIA A LA RODADURA.
La fuerza necesaria para vencer la resistencia de rodadura, F_r, es
F_r=\mu\times N
donde \mu es el coeficiente de resistencia a la rodadura, y N es la componente normal al suelo, mg cos \alpha, del peso del vehículo. Así,
F_r=\mu mg cos \alpha
FUERZA EN LA SUBIDA (O BAJADA) DE UNA PENDIENTE
La fuerza en la subida (o bajada) de una pendiente, F_p, es
F_p= \pm mg sen\alpha
En esta ecuación se emplea el signo “-” cuando F_p y F_v tengan distinto sentido (cuando el vehículo sube), y “+” cuando tengan el mismo sentido (cuando el vehículo baja).
FUERZA NECESARIA PARA VENCER LA RESISTENCIA AERODINÁMICA
La fuerza necesaria para vencer la resistencia aerodinámica, F_a, es
F_a= \frac{1}{2}C_x\rho AC^2
donde C_x es el coeficiente de resistencia aerodinámica, \rho es la densidad del aire, A es la superficie frontal del vehículo y C es la velocidad a la que se mueve el vehículo en relación con la velocidad del aire en cuyo seno se mueve.
El aire atmosférico cumple bastante bien la ecuación de estado de gas ideal, por lo que se puede escribir
pv=RT
Y como v=1/\rho, queda \frac{p}{\rho}=RT, de donde resulta
\rho = \frac{p}{RT},
quedando, para la fuerza necesaria para vencer la resistencia aerodinámica,
F_a= \frac{1}{2} C_x \frac{p}{RT} A C^2
FUERZA EJERCIDA POR EL VEHÍCULO
En la figura, es F_v.
ECUACIÓN DE NEWTON
\Sigma \overrightarrow{F}= m \frac{d \overrightarrow{C}}{dt}
Aunque es mandatorio el empleo de vectores, como todas las fuerzas se encuentran en la misma dirección, se puede trabajar escalarmente considerando simplemente sus signos, resultando,
F_v - \left(\pm mg sen\alpha + \mu mg cos \alpha + \frac{1}{2} C_x \frac{p}{RT} A C^2 \right) = m \frac{dC}{dt}
Multiplicando la ecuación anterior por la velocidad, C ,
F_v C - \left(\pm mgC sen\alpha + \mu mgC cos \alpha + \frac{1}{2} C_x \frac{p}{RT} A C^3 \right) = m C \frac{dC}{dt}
En esta ecuación, F_v C es la potencia desarrollada por el vehículo, \pm mgC sen\alpha es la potencia requerida para subir la pendiente (o aportada en la bajada, lo que es importante en los vehículos eléctricos, que pueden emplear la energía generada para cargar baterías), \mu mgC cos \alpha es la potencia requerida para vencer la resistencia a la rodadura, \frac{1}{2} C_x \frac{p}{RT} A C^3 es la potencia requerida para vencer la resistencia aerodinámica (nótese que aumenta con el cubo de la velocidad) y m C \frac{dC}{dt} es la potencia requerida en la aceleración u obtenida en la frenada que, en el caso de los vehículos eléctricos, se puede emplear en la carga de las baterías.
Fábrica de combustible nuclear en Juzbado, Salamanca.
Muchas personas, en Salamanca, creen que las instalaciones de ENUSA, en Juzbado, son una Central Nuclear. A nuestro pesar, no lo es. Una Central Nuclear aporta un valor añadido gigantesco a la zona en la que se encuentra. Aunque no por ello las instalaciones de ENUSA son menos importantes.
En ENUSA se fabrica el combustible que se emplea en los reactores de muchas Centrales Nucleares españolas y extranjeras. También, muchas personas asocian la palabra “nuclear” con Chernobyl, Fukushima… o sea, con catástrofe. Y lo que sigue, a continuación, son manifestaciones y protestas basadas en la más profunda ignorancia, que acaban llevando al poder Legislativo a escribir cosas, en forma de Reales Decretos, que a veces contienen altas dosis de irracionalidad y desconocimiento, pero que a la gran masa, acaban gustando. Cada cual es muy dueño de creerse lo que quiera y de expresarse como quiera, pero nosotros, como Ingenieros, estamos obligados a conocer cómo funcionan las cosas y si nos manifestamos, hacerlo desde el conocimiento y no desde la demagogia que hoy en día tanto manipula.
El mapa actual de Centrales Nucleares en España se muestra a continuación (aunque Garoña ya se encuentra en proceso de desmantelamiento):
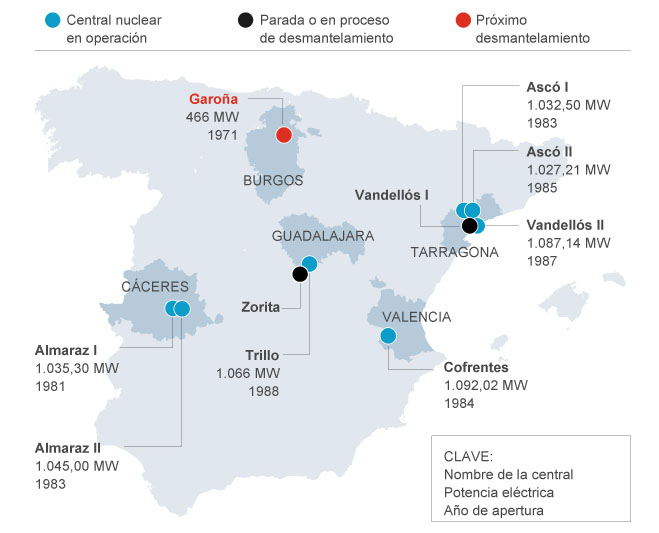
Cualquier artilugio construido por seres humanos está expuesto a accidentes. Pero no focalicemos nuestra atención en las Centrales Nucleares. Por poner un ejemplo simple, nos montamos en nuestros coches a sabiendas de que es el medio de transporte más inseguro. Las Centrales Nucleares españolas no son comparables ni a Chernobyl ni a Fukushima. Aunque el “deporte nacional” de los españoles sea la crítica total, demoledora y absolutamente destructiva de todo lo nuestro, en ese ámbito podemos estar tranquilos y orgullosos de cómo se hacen las cosas.
La Fábrica de Combustible Nuclear de Juzbado está aquí.
Algunos alumnos de la Escuela Politécnica Superior de Zamora (en la que estamos) han realizado allí sus Prácticas en Empresa. ¿Han vuelto enfermos? ¿La Fábrica de ENUSA en Juzbado supone algún peligro medioambiental? Bueno, pues echa un vistazo a este vídeo, en el que se va a responder a estas preguntas.
En mis clases no profundizo más sobre este tema porque considero que ese profundizaje corresponde más a profesores de áreas más vinculadas con la Química o la Química Técnica, aunque como se puede ver en el vídeo, el proceso de Fabricación tiene mucho interés para los estudiantes de Ingeniería, porque no es distinto de los procesos de Fabricación que estudian en sus clases.
¿Tienes contratada la potencia eléctrica que realmente necesitas? ¿O tienes demasiada potencia eléctrica contratada?
Hasta la llegada del llamado “contador inteligente” esto era relativamente fácil porque sólo era cuestión de sumar las potencias de los aparatos enchufados. Sin embargo, la falta de registro temporal de la medida lo convertía en poco menos que un enigma. Pero ahora podemos responder a esta pregunta de una forma relativamente fácil porque con el “contador inteligente”, queda el registro y se puede ver. A ver si sabemos encontrarlo. Hay que buscarlo en la web de la distribuidora, no en la de la compañía con la que tengas contratado el servicio.
Puedes ver la distribuidora que te corresponde, según la ubicación, en este mapa:
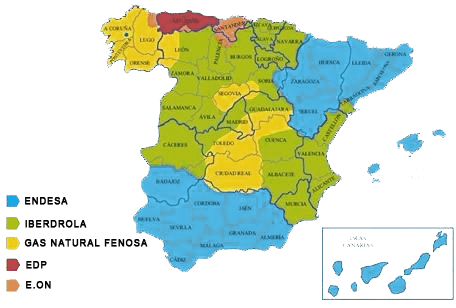
Echa un vistazo a este vínculo porque si tienes instalado el contador inteligente, puedes saber fácilmente si estás pagando por una potencia que no utilizas.
Iberdrola (distribución eléctrica).
Regístrate en esa Web si tu distribuidor es Iberdrola.
Casi todos tenemos instalada una potencia muy superior a la que necesitamos. Pero cuidado: el registro de las medidas de consumo energético hora a hora no es válido para hacerse una idea de la potencia máxima demandada, porque en una hora es posible que hayas necesitado mucha potencia en cinco minutos y poca el resto, lo que da lugar a un consumo bajo. Seria más útil un registro segundo a segundo… pero no desesperes porque con estos bueyes hay que arar y, afortunadamente, está previsto.
Vete al menú “MI CONTADOR” y haz clic en “¿Qué potencia necesito?”. Ahí verás un histórico de las potencias máximas demandadas. Esa información es suficiente. Probablemente verás que la potencia máxima demandada es bastante inferior a la potencia que tienes contratada.
Si es tu caso, cambia el término de potencia en tu Compañía Eléctrica. Actualmente se puede modificar de 100 en 100 W. No lo dudes; algo ahorrarás.
Concretamente vas a ahorrar 0,117966 €/kW día, que es el precio de kW a día de hoy, y que durante 30 días son 3,53898 €/mes. No es mucho, pero en un año son 42,46776 €… y mejor en tu bolsillo.
Freno de un avión (A319), con la reversa (en tierra).
Es un poco largo y, al principio, hasta diría que aburrido. Normalmente, volar es afortunadamente aburrido. Pero en el minuto 5 el avión llega al suelo con los slats abiertos (y también los flaps, aunque no se vean) y se ve como suben los aerofrenos y se abre la reversa del motor.
¿Qué tiene esto que ver con la resistencia aerodinámica? ¿En qué términos influye? ¿Y con el empuje en un turbofán, que calculamos en Ingeniería Térmica II?
Otra forma de la reversa (más antigua). Vete al minuto 2:20 si te da mucho aburrimiento la espera (insisto en que volar es afortunadamente aburrido):
Y aquí se puede ver la operativa del Comandante y del Segundo, en cabina, con la vista de los planos y del frente:
Producción de motores eléctricos Audi.
¿Por qué vemos indicadores de temperatura y humedad en recintos públicos?
Por el Real Decreto 1826/2009, de 27 de noviembre, por el que se modifica el Reglamento de instalaciones térmicas en los edificios, aprobado por Real Decreto 1027/2007, de 20 de julio.
 Cargando...
Cargando...
