Desde el 14 de Marzo nos encontramos en España en Estado de Alarma por la preocupante evolución del número de contagiados por el COVID-19, que ha mostrado ser exponencial.
¿Por qué la evolución del número de contagios del del COVID-19 es exponencial? En esta página Web se muestran algunas animaciones de todos los escenarios posibles. Las animaciones siempre se agradecen pero en Ingeniería necesitamos ponerles números a las cosas.
Vamos a ello:
Aparecen más infectados cuantos más infectados haya.
Llamando [i] al número total de infectados (lo que en Química sería la “concentración” de infectados), esto lleva a admitir que la velocidad de contagio, \frac{d[i]}{dt}, es proporcional al número de contagiados, k[i]. La Cinética Química del número de contagiados corresponde, si esto es así, a la de una reacción de orden 1, es decir
\frac{d[i]}{dt}=k[i]
Se trata de una ecuación diferencial de variables separables en la que la constante k tiene unidades de \frac{1}{t} . No es necesario, en este caso, recurrir al Sistema Internacional y expresar el tiempo en segundos. Basta con expresarlo en días, ya que el balance de infectados se ofrece diariamente. Por tanto, las unidades de k serán \frac{1}{\text{dias}} . La ecuación diferencial anterior lleva a
\frac{d[i]}{[i]} = k dt
Integrando entre dos concentraciones de infectados, [i]_1 e [i]_2 , reportadas en dos instantes, t_1 e t_2 , resulta
\int _{[i]_1}^{[i]_2}\frac{d[i]}{[i]} = \int _{t_1}^{t_2} k dt
Considerando k como constante, resulta
\ln \frac{[i]_2}{[i]_1}=k \left(t_2-t_1\right)
Y operando, resulta
\frac{[i]_2}{[i]_1}=e^{k \left(t_2-t_1\right)}
Nuestro problema, ahora, es determinar el valor de la constante k . Para ello, hemos de recurrir a los datos medidos de dos instantes cualesquiera. En Web del Ministerio de Sanidad se pueden encontrar datos fiables. Basta con elegir los datos correspondientes a dos días, cualesquiera, y sustituir en la ecuación
k=\frac{\ln \frac{[i]_2}{[i]_1}}{t_2-t_1}
Tomando los datos del día 16 de Marzo, cuando [i]_1=9191 infectados, y del 25 de Marzo (a 9 días de distancia), cuando [i]_2=47610 infectados, resulta
k=\frac{ln \frac{47610 \text{infectados}}{9191 \text{infectados}}}{9 \text{días}}=0, 1828 \text{días}^{-1}
Así pues, la ecuación que da una idea de la evolución de la infección es
[i]_2=[i]_1e^{0,1828 \left(t_2-t_1\right)}
donde hay que escribir los tiempos en días.
A continuación se muestra la representación gráfica de esta ecuación. Como se puede ver, es una representación típica de una ecuación exponencial. Pasada una primera fase inicial, en la que el número de infectados aumenta lentamente, pasa a una fase de aumento muy rápido… y rapidísimo a medida que avanza el tiempo.
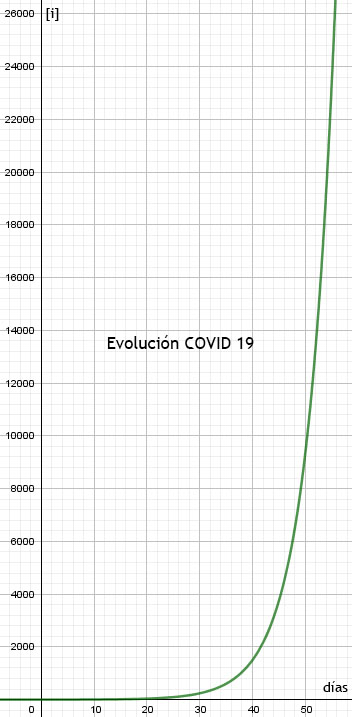
Como se puede deducir de la forma de la curva, el aumento del número de infectados, [i], es muy lento en los primeros días. Esto es lo que ha enmascarado la epidemia y lo que ha confundido a los expertos: al tratarse de un virus nuevo, nadie era capaz de imaginarse su altísima contagiosidad. En España no miramos a la evolución del COVID-19 en otros países (o sí) y jamás pensamos que íbamos a seguir el mismo camino. La cuestión es que aquí estamos.
Las actuaciones, a la vista de la forma de la curva, se encaminan a sacarla de la zona exponencial. Las primeras medidas, en las que estamos, tratan de encontrar un cambio en la ya leve curvatura de la gráfica, es decir, una inflexión. Una inflexión que será muy tenue, pero aparecerá. Y, a partir de ahí, a encontrar el máximo de la función. A partir del máximo, nos encontraremos en ya en la zona de decrecimiento de los contagios. A partir de ahí, iremos “viendo la luz”.
En este sentido, la declaración del Estado de Alarma y las medidas de contención son mucho más que acertadas y pertinentes. Hay que “doblar” (textual del Prof. Dr. Fernando Simón Soria) la ecuación exponencial; véanse los escenarios recreados en las animaciones de Washington Post que indiqué en el comienzo de esta misma entrada.



